In the diverse fields of science and engineering, solving equations is a fundamental task. An equation with one variable is typically expressed in the form:
f ( x ) = 0
A "solution" or "root" of the equation is a specific numerical value assigned to x that makes the equation true. In other words, when x is substituted into f ( x ) , the result is zero.
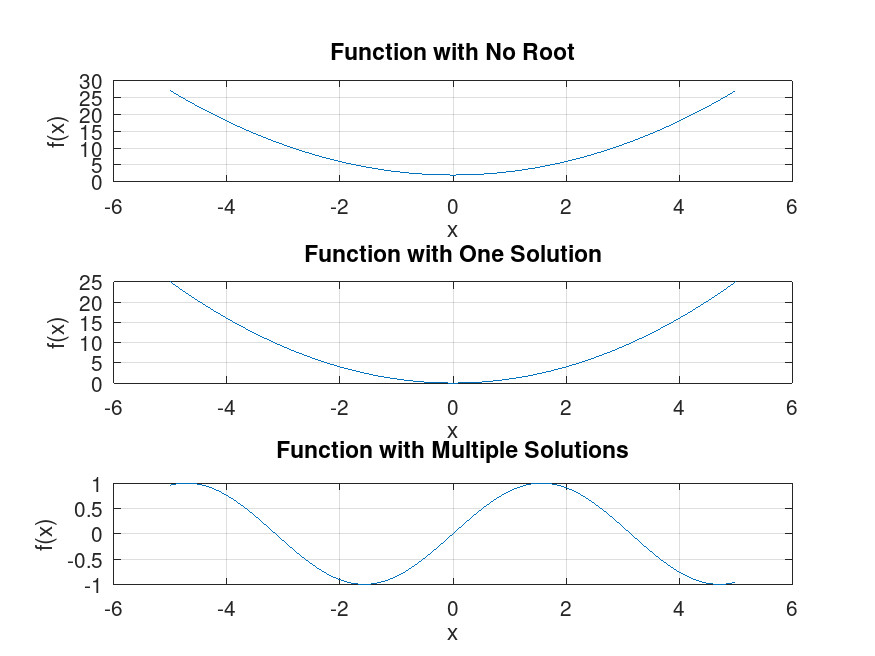
From a graphical perspective, as depicted in the figure below, the solution corresponds to the point(s) where the curve representing the function f ( x ) intersects or touches the x-axis. At these points, the value of f ( x ) is zero.
It’s important to note that an equation may not have any solutions, meaning there are no points at which f ( x ) crosses the x-axis. Alternatively, an equation can have a single unique solution or multiple solutions. In some cases, there can be infinitely many roots, especially when dealing with periodic functions or certain types of algebraic equations.
The number of solutions an equation has depends on the nature of the function f ( x ) . For instance, linear equations typically have a single solution, quadratic equations can have up to two solutions, and higher-degree polynomials may have multiple solutions corresponding to their degree.
Solving equations is a common task in mathematics, and when the equation is straightforward, the value of the variable x can often be found through direct mathematical operations or by applying a known formula. For instance, the quadratic formula can be used to find the exact solutions for x in a quadratic equation.
However, there are many instances where finding an analytical solution—that is, a precise algebraic expression for x —is not feasible. This often occurs with more complex equations or functions. Take, for example, the equation that calculates the area A_S of a circular segment with radius r :
A_S = 1 / 2 r^ 2 ( θ - sin ( θ ) )
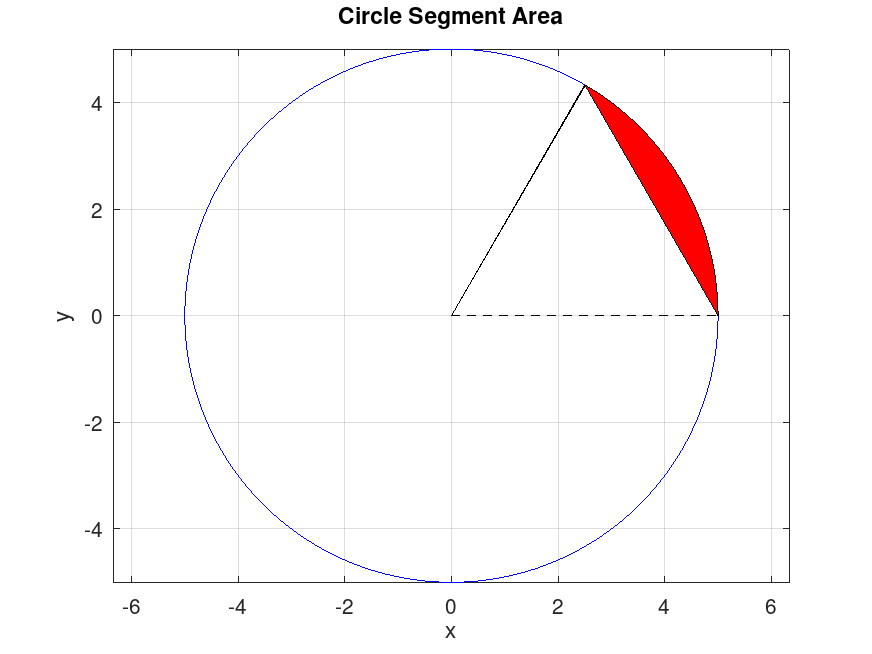
If you know the values of A S and r , and you need to find the angle θ , you would have to solve this equation for θ . Unfortunately, there’s no straightforward algebraic way to isolate θ in this equation.
In such cases, we turn to numerical methods to find an approximate solution. A numerical solution for an equation f ( x ) = 0 is a value of x that makes f ( x ) very close to zero. It won’t be exactly zero but within an acceptable margin of error that we define as "close enough."
For example, if we have a circle with radius r = 3 m and segment area A S = 8 m 2 , we can express our problem as:
f ( θ ) = 8 - 4.5 ( θ - sin ( θ ) ) = 0
By plotting f ( θ ) , we might observe that the solution lies between 2 and 3 radians.
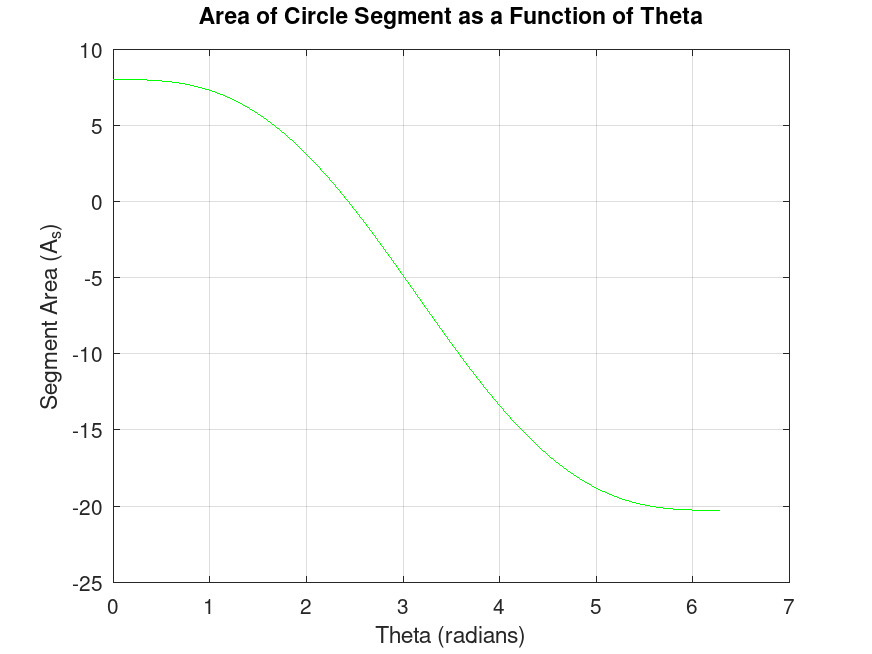
If we try θ = 2.4 radians, we get f ( θ ) = 0.2396 , which is close but not quite zero. If we refine our guess to θ = 2.43 radians, we get f ( θ ) = 0.003683 , which is much closer to zero and thus a more accurate approximation.
It’s important to understand that while we can get very close, it’s typically impossible to find a numerical value for θ that makes f ( θ ) exactly zero. The goal of numerical methods is to find a value that makes f ( x ) sufficiently small—how small depends on the level of accuracy we desire for our solution.
Methods for Solving Nonlinear Equations Numerically
Unlike analytical solutions that provide exact formulas to solve equations, numerical solutions offer approximate answers. We achieve this approximation through a step-by-step process called iteration, where we start with an educated guess for the solution and then use specific methods to get closer and closer to the true answer.
There are two main categories for numerical solution techniques: bracketing methods and open methods. Bracketing methods, like the bisection method and the method of false position (regula falsi), require us to identify an interval that guaranteedly contains the solution (the root of the equation). These methods then work by repeatedly halving this interval, effectively squeezing in on the true solution. While bracketing methods are guaranteed to converge on an answer, they might take more steps to reach a desired level of accuracy.
Open methods, on the other hand, take a different approach. Techniques like the Newton-Raphson method and the secant method begin with an initial guess close to the solution. They then use a specific formula to refine this guess iteratively, meaning they keep repeating the calculation with the improved value from the previous step. Open methods can be more efficient than bracketing methods, but they come with a caveat: they might not always converge to a solution for certain types of equations.
In cases where an equation has multiple solutions (roots), we need to find them one at a time. We can employ the same numerical techniques we discussed earlier, but we would need to start with a different initial guess for each root to isolate and solve for them individually.
Since numerical solutions are approximations, it’s crucial to consider the error involved. The absolute error tells us the actual difference between the approximate solution we obtain and the true solution. The relative error, however, expresses this difference as a proportion of the true solution, giving us a better sense of the magnitude of the error relative to the actual answer. To control the accuracy of our solution, we can set a tolerance level, which defines the acceptable amount of error.
We will discuss specific methods like bisection method, regula falsi, Newton-Raphson method, secant method, and fixed-point iteration in future blog posts. These explorations will include details on how to implement these methods and important practical considerations to keep in mind when using them. Feel free to ask any questions you have along the way!