Solving Nonlinear Equation Using Regula Falsi Method

Introduction

In many science and engineering there is occasions that we need to solve nonlinear equation, that is find the roots of an equation, which is the points where the equation graph meets the x axis. The regula falsi method (also called false position and linear interpolation methods) is a bracketing method for finding a numerical solution of a nonlinear equation of the form f(x) = 0.

Formulation

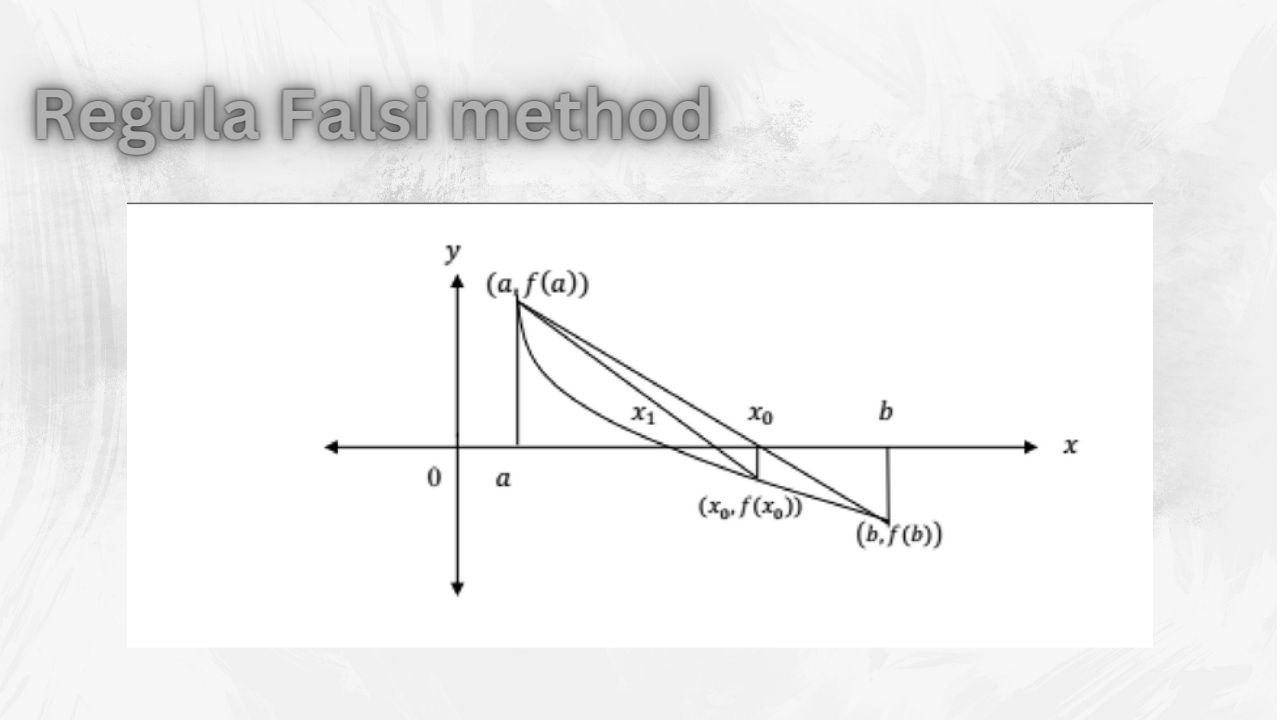
Algorithm For Regula Falsi Method

When Should the Bisection Process Stopped?

An Example

The Python Program

The python program for solving this equation is listed here:

def regula_falsi(f, a, b, tol):
  """
  This function implements the Regula Falsi method to find an approximate root of a nonlinear equation.

  Args:
      f: The function for which we want to find the root.
      a: Lower bound of the initial interval.
      b: Upper bound of the initial interval.
      tol: Tolerance level for the approximation.

  Returns:
      The approximate root of the equation within the given tolerance.
  """
  fa = f(a)
  fb = f(b)
  if fa * fb > 0:
    print("The given interval does not contain a root.")
    return None
  
  iterations = 0
  while abs(b - a) > tol:
    c = (a * fb - b * fa) / (fb - fa)
    fc = f(c)
    if fa * fc < 0:
      b = c
    else:
      a = c
    iterations += 1
  
  print(f"Root found approximately after {iterations} iterations: x = {c}")
  return c

# Define the function
def f(x):
  return x**3 - x - 1

# Set initial interval and tolerance
a = 1
b = 2
tol = 0.001

# Find the approximate root
root = regula_falsi(f, a, b, tol)

if root:
  print(f"f({root}) = {f(root):.4f}")

Explanation:

1. The regula_falsi function takes the equation (f), the initial interval (a, b), and the tolerance (tol) as input.
2. It checks if the function values at a and b have the same sign. If they do, there’s no root in the interval (since the function goes from positive to negative or vice versa when the root is crossed).
3. It iteratively calculates a new point (c) within the interval based on the function values at a and b. This is essentially the x-intercept of the line connecting the points (a, f(a)) and (b, f(b)).
4. It checks the signs of f(a) and f(c). If they are opposite, the root lies between a and c, so we update the upper bound (b) to c. Otherwise, the root lies between c and b, so we update the lower bound (a) to c.
5. This process continues until the difference between a and b becomes less than the tolerance (tol), indicating we’re close enough to the root.
6. The function then prints the number of iterations and the approximate root along with its function value (f(root)) for verification (ideally close to zero).

This program demonstrates how to use the Regula Falsi method to solve the given cubic equation ( f ( x ) = x 3 - x - 1 = 0 ). You can modify the code to try the method with other nonlinear equations by changing the definition of the f function.

Additional Notes About Regula falsi Method

• The method always converge to an answer, if a root is trapped in the interval [ a , b ] .
• Frequently, the function in the interval [ a , b ] is either concave up or concave down. In this case, one of the endpoints of the interval remains the same during the iteration, while the other endpoint advances to ward the root. In other words, the numerical solution advances toward the root only from one side. The convergence toward the solution could be faster if the other endpoint would also move toward the root. Several modifications have been introduced to the regula falsi method that makes the sub-interval in successive iteration approach the root from both sides. We will discuss these methods in later blog posts.