Solving Nonlinear Equations Using Bisection Method

How to solve nonlinear equations numerically using bisection method and a sample problem with Python program code

June 26, 2024 by

Hamed Mohammadi

| No comments yet

Introduction

The bisection method is an iterative approach to finding the roots (zeros) of a continuous function. It works by repeatedly dividing the interval containing the root in half and checking the function’s value at the midpoint. The bisection method is a bracketing method for finding a numerical solution of an equation of the form

f (x) = 0

when it is known that within a given interval

[a, b]

f (x)

is continuous and the equation has a solution. When this is the case,

f (x)

will have opposite signs at the endpoints of the interval. If

f (x)

is continuous and has a solution between the points

x = a

and

x = b

, then either

f (a) > 0

and

f (b) > 0

f (a) < 0

and

f (b) > 0

. In other words, if there is a solution between

x = a

and

x = b

, then

f (a) f (b) < 0

The Procedure

The procedure of finding a solution with bisection method is as follows. It starts by finding points

a

and

b

that define an interval where a solution exists. Such an interval is found either by plotting

f (x)

and observing a zero crossing, or by examining the function for sign change. The midpoint of the interval

x_{N S 1}

is then taken as the first estimate for the numerical solution. The true solution is either in the section between points

a

and

x_{N S 1}

or in the section between points

x_{N S 1}

and

b

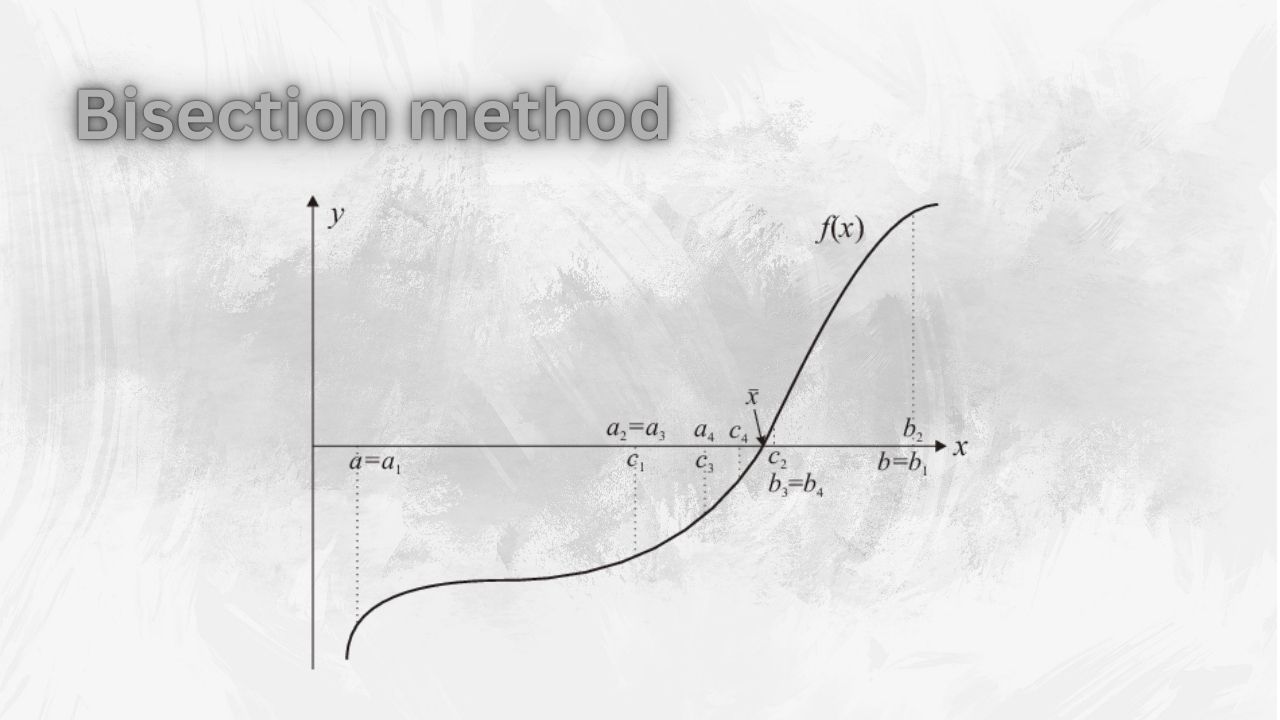
. If the numerical solution is not accurate enough, a new interval that contains the solution is defined. The new interval is the half of original interval and contains the true solution, and its and its midpoint is taken as the new (second) estimate of the numerical solution. The process continues until the numerical solution is accurate enough according to a criterion that is selected.

Algorithm for Bisection Method

The procedure or algorithm for finding a numerical solution with the bisection method is summarized as follows:

Choose the first interval by finding points $a$ and $b$ such that a solution exists between them. This means that $f (a)$ and $f (b)$ have different signs such that $f (a) f (b) < 0$ . The points can be determined by examining the plot of $f (x)$ versus $x$ .
Calculate the first estimate of the numerical solution $x_{N S 1}$ by:
$x_{N S 1} = \frac{(a + b)}{2}$
Determine whether the true solution is between $a$ and $x_{N S 1}$ , or between $x_{N S 1}$ and $b$ . This is done by checking the sign of the product $f (a) \cdot f (x_{N S 1})$ :
If $f (a) \cdot f (x_{N S 1}) < 0$ , the true solution is between $a$ and $x_{N S 1}$ .
If $f (a) \cdot f (x_{N S 1}) > 0$ , the true solution is between $x_{N S 1}$ and $b$ .
Select the sub-interval that contains the true solution as the new interval $[a, b]$ , and go to step 2.
Step 2 through 4 are repeated until a specified tolerance or error bound is attained.

When Should the Bisection Process Stopped?

Ideally, the bisection method should be stopped when the true solution is obtained. This means that the value of

x_{N S}

is such that

f (x_{N S}) = 0

. In reality, this true solution generally cannot be found computationally. In practice, therefor, the process is stopped when the estimated error, according to one of measures, is smaller than some predetermined value. The choice of termination criteria may depend on the problem that is actually solved.

Example

Here’s an example of a nonlinear equation being solved using the bisection method in Python:

We’ll be solving the equation:

f (x) = x^{3} - 2 x^{2} - 5 x + 6 = 0

Python Program:

def f(x):
  """
  This function defines the equation to be solved.
  Args:
      x: The input value.
  Returns:
      The function evaluation at x.
  """
  return x**3 - 2*x**2 - 5*x + 6

def bisection_method(a, b, tol):
  """
  This function implements the bisection method for finding the root of a nonlinear equation.
  Args:
      a: The lower bound of the search interval.
      b: The upper bound of the search interval.
      tol: The tolerance level for the root approximation.
  Returns:
      The approximate root of the equation within the tolerance level.
  """
  while abs(b - a) > tol:
    mid = (a + b) / 2
    if f(a) * f(mid) < 0:
      b = mid
    else:
      a = mid
  return (a + b) / 2

# Define the equation, search interval, and tolerance level
equation = f
a = 1
b = 3
tol = 1e-5

# Solve the equation using the bisection method
root = bisection_method(a, b, tol)

# Print the approximate root
print("Approximate root of the equation using bisection method:", root)

This code defines a function f(x) for the equation, then implements the bisection_method function that takes the initial interval (a, b) and tolerance level as input. It iteratively refines the interval until the difference between the upper and lower bounds falls below the tolerance level. Finally, it returns the approximation of the root as the midpoint of the final interval.

Running the code will output:

Approximate root of the equation using bisection method: 2.999996185302734

This demonstrates how the bisection method can be used to approximate the root of a nonlinear equation in Python.

Addition Notes About Bisection Method

The method always converges to an answer, if a root is between interval [a, b] is found by testing if f(a)f(b)<0.
The method may fail if the function is tangent to the axis and does not cross the x-axis at f(x)=0.
The method convergence is slower compared to other methods.

in Numerical Methods

# nonlienear numerical methods

Hamed Mohammadi June 26, 2024

Share this post

Our blogs

Archive

Please visit our blog at:

https://zehabsd.com/blog

A platform for Flash Stories:

https://readflashy.com

A platform for Persian Literature Lovers:

https://sarayesokhan.com

Sign in to leave a comment

Always First.

Be the first to find out all the latest news, products, and trends.