1 Introduction
Nonlinear equations, unlike their linear counterparts, can’t be solved with simple algebra. But fear not, for Newton’s method comes to the rescue! This iterative technique is a powerful tool for finding the roots (also called zeros) of these nonlinear equations.
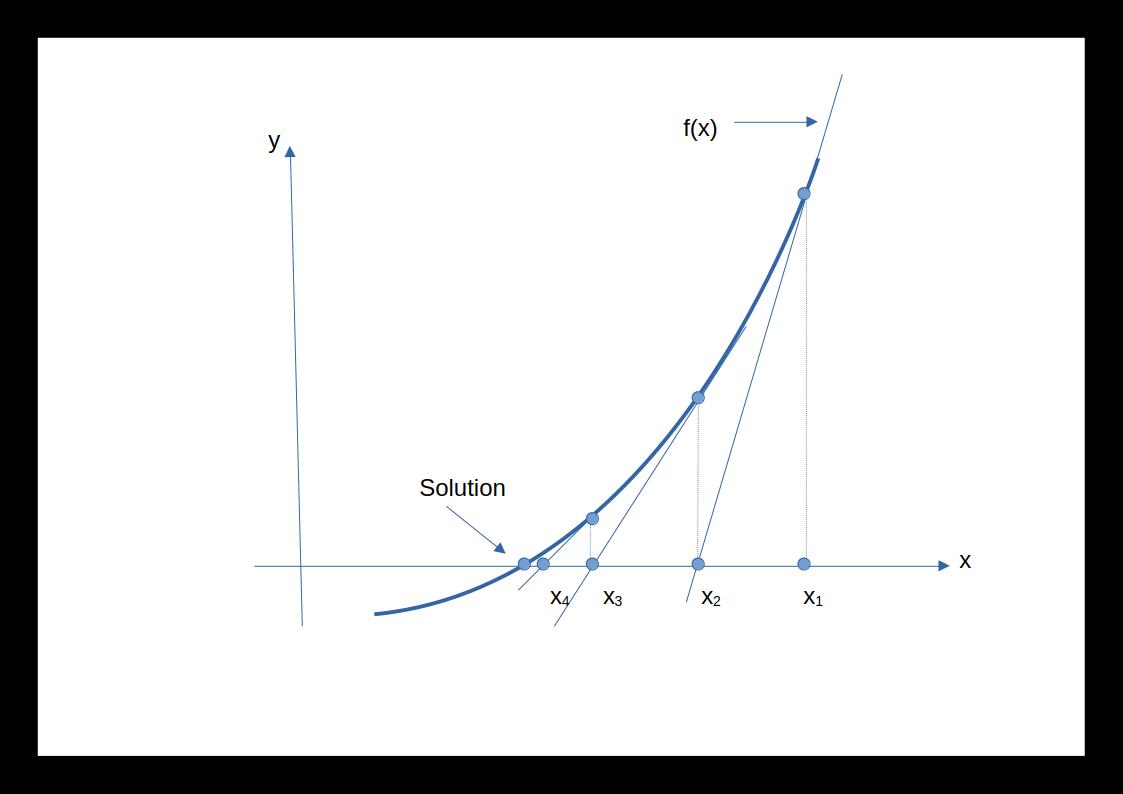
Imagine a curvy graph and you’re looking for the x-value where the graph intersects the x-axis (i.e., the root). Newton’s method works by taking an initial guess for this x-value. Then, it cleverly uses the concept of the tangent line: it draws a line tangent to the curve at your guess, and finds where this tangent line meets the x-axis. This new x-axis intercept becomes a better approximation for the root.
The beauty lies in the repetition. You keep using the same idea, drawing a tangent line at your new guess, and iteratively getting closer and closer to the actual root. With each step, the approximation gets refined, leading to a more accurate solution.
Newton’s method or Newton-Raphson method is a numeric method for finding a numerical solution of an equation of the form f(x) = 0 where f(x) is continuous and differentiable and also it is know that the equation have a solution approximate to a given point. The method is shown in figure below.
2 Algorithm for Newton-Raphson Method
Algorithm for Newton-Raphson method is simple:
- Choose a point x 1 as an initial guess of the solution.
- For each iteration until the error is smaller than a specified value, calculate the next solution using the formula in the last section.
3 When Should Iterations Stop?
Sample Problem: Finding the Square Root
Let's use Newton's method to find the square root of a number (say, 2). The square root of a number x satisfies the equation x^2 - y = 0, where y is the desired square root. We can rewrite this as f(y) = y^2 - 2 = 0.
Here's the Python program to solve it:
def f(y): """Function representing the equation (y^2 - 2 = 0).""" return y**2 - 2 def df(y): """Derivative of the function f(y) (2*y).""" return 2*y def newton_method(f, df, x0, tol, max_iter): """ Implements Newton's method for finding the root of a function. Args: f: The function for which we want to find the root. df: The derivative of the function f. x0: The initial guess for the root. tol: The tolerance level for convergence. max_iter: The maximum number of iterations allowed. Returns: The root (if found) or None. """ for i in range(max_iter): x_new = x0 - f(x0) / df(x0) if abs(x_new - x0) < tol: return x_new x0 = x_new return None # Define initial guess, tolerance, and max iterations x_guess = 1.0 # Initial guess (can be adjusted) tolerance = 1e-6 max_iterations = 10 # Solve for the square root using Newton's method root = newton_method(f, df, x_guess, tolerance, max_iterations) if root: print(f"Square root of 2 (approximately): {root:.6f}") else: print(f"No root found within tolerance or {max_iterations} iterations.")
This program defines the function f(y) and its derivative df(y) representing the equation y^2 - 2 = 0. The newton_method function remains the same. It then defines the initial guess, tolerance, and maximum iterations. Finally, it calls the newton_method to find the root and prints the result.
This example demonstrates how to apply Newton's method to solve a simple nonlinear equation. You can modify the f(y) and df(y) functions to solve other nonlinear equations following the same approach.